
The following will help access element of the third column C(:,3) Multiply Matrices I will use the following to access the element on the first rows-second column.
Matlab transpose code#
If I need to access the first row of the Matrix, I will use the following code C(1,:) You can individually access element of a Matrix or a whole vector.
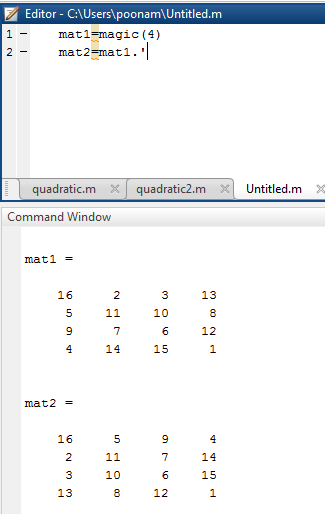
To find the transpose of a Matrix, use the following A' To find the first lower diagonal use diag(A,-1) To find the first upper diagonal use diag(A,1) To find the main diagonal of A, we will use diag(A) Where (3,2) is the size of the Matrix Find the diagonal of a MatrixĭIAG help access diagonals of Matrices in Matlab. To create a Matrix with Random element in Matlab, use rand(3,2) To find the determinant of a Matrix in Matlab, use the following code det(A) Define a Matrix with Random elements To find the inverse of a Matrix, use the code: inv(A) Find the determinant of a Matrix Remember both matrices need to have the same size. To divide two Matrices element by element use the following A./C Now we can add A and C using the following code A+C Divide Matrices element by element So, let’s create a new Matrix C with the same size as A To add two matrices A and B, we need size(A) to be identical to size(B) Note A here is the matrix we created in the previous step. To find the size of a Matrix, use the following code size(A) The size of a Matrix is its number of rows and columns. Write a Matrix in Matlab Find the size of a Matrix Add Matrices Divide Matrices element by element Find the inverse of a Matrix Find the determinant of a Matrix Define a Matrix with Random elements Find the diagonal of a Matrix Compute the Transpose of a Matrix Extract an element in a Matrix Multiply Matrices Multiply 2 Matrices element by element Create a Matrix with all elements equal to zero Create a Matrix with All elements equal to one Matlab Matrix Operations Write a Matrix in MatlabĪfter pressing ENTER, here is how it will look in Matlab window Find the size of a Matrix
Matlab transpose how to#
In this read, we will hand over to you some basic Matlab Matrix operation and how to use them to get what you want.
Matlab transpose software#
With Matlab, one of the major problem for beginners is to understand how the software works and what the software need in order to help them accomplish their goal using it. Here is where Matlab come to play, it makes working with Matrices easier. If you'd like to learn more, it's worth reading about representation theory.If you ever tried to work with huge matrices, you will know how unpleasant and tedious. Hence - when you transpose a matrix over the complex numbers, Matlab helpfully completes the job by conjugating the elements for you as well. It just so happens that for historical reasons we developed the algebraic form using the symbols j or i first, and invented the idea of conjugation, which is really just a special case of the transpose.

If you like, the natural representation is the 2nx2n real form.
It's not surprising that we don't find it in natural laws!

With this in mind, I'd say that the "ordinary transpose" of a matrix over the complex numbers is actually a very strange thing. In fact I'll go further and claim (without proof) that any vector or matrix over the complex numbers has an isomorphism in vectors/matrices over the reals (the latter having double the dimensionality), and that conjugate-transposition in the complex version is identical to transposition in the real version. What happens if we have an nxn matrix of complex numbers? Why then we can just represent it as a 2nx2n matrix of real numbers, where each 2x2 sub-matrix is of the form xI + yJ! Turns out if you do so that the Hermitian (conjugate) transpose of the nxn complex matrix is just equivalent to the ordinary transpose in the 2nx2n real form. So conjugating the complex number was the same operation as transposing its matrix representation. Then we have this equivalence (using j to denote the imaginary unit): x + yj xI + yJ Let I = (1 0) J = (0 -1)Īnd notice that the transpose of J ( J^T) is just equal to -J. Consider a matrix representation of complex numbers. Actually I'd argue that there are deep reasons why the transpose IS the conjugate.


 0 kommentar(er)
0 kommentar(er)
